Optimal computing budget allocation

}} In computer science, optimal computing budget allocation (OCBA) is an approach to maximize the overall simulation efficiency for finding an optimal decision. It was introduced in the mid-1990s by Dr. Chun-Hung Chen.

OCBA determines the number of replications or the simulation time that is needed in order to receive acceptable or best results within a set of given parameters. This is accomplished by using an asymptotic framework to analyze the structure of the optimal allocation.

OCBA has also been shown effective in enhancing partition-based random search algorithms for solving deterministic global optimization problems.

Intuitive explanation

OCBA's goal is to provide a systematic approach to run a large number of simulations including only the critical alternatives in order to select the best alternative.

In other words, OCBA focuses on only part the most critical alternatives, which minimizes computation time and reduces these critical estimators’ variances. The expected result maintains the required level of accuracy, while requiring less amount of work.

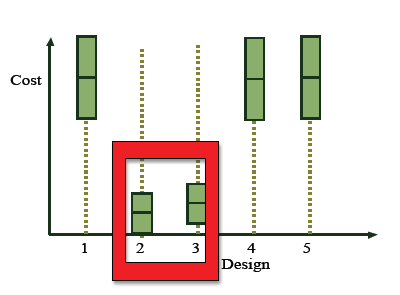
For example, we can create a simple simulation between five alternatives. The goal is to select an alternative with minimum average delay time. The figure below shows preliminary simulation results ( i.e. having run only a fraction of the required number of simulation replications). It is clear to see that alternative 2 and 3 have a significantly lower delay time (highlighted in red). In order to save computation cost (which is time, resources and money spend on the process of running the simulation) OCBA suggests that more replications are required for alternative 2 and 3, and simulation can be stopped for 1, 4, and 5 much earlier without compromising results.

Observing the above graphic, it is clear that alternative 2 and 3 have the lowest cost. OCBA suggests to run further simulations on only alternatives 2 and 3 in order to minimize computation cost

Problem

The main objective of OCBA is to maximize the probability of correct selection (PCS). PCS is subject to the sampling budget of a given stage of sampling τ.

[math]\displaystyle{ \begin{align} \max_{\tau_1,\tau_2,\ldots,\tau_k} &\mathrm{ PCS} \\ \text{subject to } &\sum_{i=1}^k \tau_i=\tau,\\ & \tau_i \ge 0, i=1,2,...,k.\qquad (1) \end{align} }[/math]

In this case [math]\displaystyle{ \sum_{i=1}^k \tau_i=\tau }[/math] stands for the total computational cost.

Some extensions of OCBA

Experts in the field explain that in some problems it is important to not only know the best alternative among a sample, but the top 5, 10, or even 50, because the decision maker may have other concerns that may affect the decision which are not modeled in the simulation.

According to Szechtman and Yücesan (2008), OCBA is also helpful in feasibility determination problems. This is where the decisions makers are only interested in differentiating feasible alternatives from the infeasible ones. Further, choosing an alternative that is simpler, yet similar in performance is crucial for other decision makers. In this case, the best choice is among top-r simplest alternatives, whose performance rank above desired levels.

In addition, Trailovic and Pao (2004) demonstrate an OCBA approach, where we find alternatives with minimum variance, instead of with best mean. Here, we assume unknown variances, voiding the OCBA rule (assuming that the variances are known). During 2010 research was done on an OCBA algorithm that is based on a t distribution. The results show no significant differences between those from t-distribution and normal distribution. The above presented extensions of OCBA is not a complete list and is yet to be fully explored and compiled.

Multi-objective OCBA

Multi-objective Optimal Computing Budget Allocation (MOCBA) is the OCBA concept that applies to multi-objective problems. In a typical MOCBA, the PCS is defined as

[math]\displaystyle{ \Pr\{CS\} \equiv \Pr \left\{ \left( \bigcap_{i \in S_p} E_i \right) \bigcap \left( \bigcap_{i \in \overline{S}_p} E_i^c \right) \right\}, }[/math]

in which

• [math]\displaystyle{ S_p }[/math] is the observed Pareto set,
• [math]\displaystyle{ \overline{S}_p }[/math] is the non-Pareto set, i.e., [math]\displaystyle{ \overline{S}_p = \Theta \backslash S_p }[/math],
• [math]\displaystyle{ E_i }[/math] is the event that design [math]\displaystyle{ i }[/math] is non-dominated by all other designs,
• [math]\displaystyle{ E_i^c }[/math] is the event that design [math]\displaystyle{ i }[/math] is dominated by at least one design.

We notice that, the Type I error [math]\displaystyle{ e_1 }[/math] and Type II error [math]\displaystyle{ e_2 }[/math] for identifying a correct Pareto set are respectively

[math]\displaystyle{ e_1 = 1 - \Pr\left\{ \bigcap_{i \in \overline{S}_p} E_i^c \right\} }[/math] and [math]\displaystyle{ e_2 = 1 - \Pr\left\{ \bigcap_{i \in S_p} E_i \right\} }[/math].

Besides, it can be proven that

[math]\displaystyle{ e_1 \leq ub_1 = H\left|\overline{S}_p\right| - H\sum_{i \in \overline{S}_p}{\max_{j\in\Theta, j \neq i}\left[ \min_{l \in {1,\ldots,H}} \Pr\left\{ \tilde{J}_{jl} \leq \tilde{J}_{il} \right\} \right]} }[/math]

and

[math]\displaystyle{ e_2 \leq ub_2 = (k-1) \sum_{i \in S_p}\max_{j\in\Theta,j \neq i}\left[ \min_{l\in{1,\ldots,H} } \Pr\left\{ \tilde{J}_{jl} \leq \tilde{J}_{il} \right\} \right], }[/math]

where [math]\displaystyle{ H }[/math] is the number of objectives, and [math]\displaystyle{ \tilde{J}_{il} }[/math] follows posterior distribution [math]\displaystyle{ Normal\left( \bar{J}_{il}, \frac{\sigma_{il}^2}{N_i} \right). }[/math] Noted that [math]\displaystyle{ \bar{J}_{il} }[/math] and [math]\displaystyle{ \sigma_{il} }[/math] are the average and standard deviation of the observed performance measures for objective [math]\displaystyle{ l }[/math] of design [math]\displaystyle{ i }[/math], and [math]\displaystyle{ N_i }[/math] is the number of observations.

Thus, instead of maximizing [math]\displaystyle{ \Pr\{CS\} }[/math], we can maximize its lower bound, i.e., [math]\displaystyle{ APCS{-}M \equiv 1-ub_1-ub_2. }[/math] Assuming [math]\displaystyle{ \tau\rightarrow \infty }[/math], the Lagrange method can be applied to conclude the following rules:

[math]\displaystyle{ \tau_i = \frac{\beta_i}{\sum_{j\in\Theta}\beta_j} \tau, }[/math]

in which

• for a design [math]\displaystyle{ h\in S_A }[/math], [math]\displaystyle{ \beta_h = \frac{\left(\hat{\sigma}^2_{hl_{j_h}^h} + \hat{\sigma}^2_{j_{h}l_{j_h}^h} / \rho_h\right) / {\delta^2_{hj_{h}l_{j_h}^h}}} {\left( \hat{\sigma}^2_{ml_{jm}^m} + \hat{\sigma}^2_{j_{m}l_{jm}^m} / \rho_m \right) / {\delta^2_{mj_{m}l_{j_m}^m}}} }[/math],
• for a design [math]\displaystyle{ d\in S_B }[/math], [math]\displaystyle{ \beta_d = \sqrt{\sum_{i \in \Theta_d^*} \frac{\sigma^2_{dl_d^i}}{\sigma^2_{il_d^i}}\beta_i^2} }[/math],

and [math]\displaystyle{ \delta_{ijl} = \bar{J}_{jl} - \bar{J}_{il}, }[/math]

[math]\displaystyle{ j_i \equiv \arg \max_{j\in\Theta, j \neq i} \prod_{l=1}^{H}{\Pr\left\{ \tilde{J}_{jl} \leq \tilde{J}_{il} \right\}}, }[/math]

[math]\displaystyle{ l_{j_i}^i \equiv \arg \min_{l\in{1,\ldots,H}} \Pr\left\{ \tilde{J}_{jl} \leq \tilde{J}_{il} \right\}, }[/math]

[math]\displaystyle{ S_A \equiv \left\{ design \; h\in S \mid \frac{\delta^2_{hj_hl^h_{j_h}}}{\frac{\hat{\sigma}^2_{hl^h_{j_h}}}{\alpha_h}+\frac{\hat{\sigma}^2_{j_hl^h_{j_h}}}{\alpha_{j_h}}} \lt \min_{i\in \Theta_h} \frac{\delta^2_{ihl^i_h}}{\frac{\hat{\sigma}^2_{il^i_h}}{\alpha_i}+\frac{\hat{\sigma}^2_{hl^i_h}}{\alpha_h}} \right\}, }[/math]

[math]\displaystyle{ S_B \equiv S \backslash S_A, }[/math]

[math]\displaystyle{ \Theta_h = {i | i\in S, j_i = h}, }[/math]

[math]\displaystyle{ \Theta_d^* = {h | h \in S_A, j_h = d}, }[/math]

[math]\displaystyle{ \rho_i = \alpha_{j_i} / \alpha_i. }[/math]

Constrained optimization

Similar to the previous section, there are many situations with multiple performance measures. If the multiple performance measures are equally important, the decision makers can use the MOCBA. In other situations, the decision makers have one primary performance measure to be optimized while the secondary performance measures are constrained by certain limits.

The primary performance measure can be called the main objective while the secondary performance measures are referred as the constraint measures. This falls into the problem of constrained optimization. When the number of alternatives is fixed, the problem is called constrained ranking and selection where the goal is to select the best feasible design given that both the main objective and the constraint measures need to be estimated via stochastic simulation. The OCBA method for constrained optimization (called OCBA-CO) can be found in Pujowidianto et al. (2009) and Lee et al. (2012).

The key change is in the definition of PCS. There are two components in constrained optimisation, namely optimality and feasibility. As a result, the simulation budget can be allocated to each non-best design either based on the optimality or feasibility. In other word, a non-best design will not be wrongly selected as the best feasible design if it remains either infeasible or worse than the true best feasible design. The idea is that it is not necessary to spend a large portion of the budget to determine the feasibility if the design is clearly worse than the best. Similarly, we can save the budget by allocating based on feasibility if the design is already better than the best in terms of the main objective.

Feasibility determination

The goal of this problem is to determine all the feasible designs from a finite set of design alternatives, where the feasible designs are defined as the designs with their performance measures satisfying specified control requirements (constraints). With all the feasible designs selected, the decision maker can easily make the final decision by incorporating other performance considerations (e.g., deterministic criteria, such as cost, or qualitative criteria which are difficult to mathematically evaluate). Although the feasibility determination problem involves stochastic constraints too, it is distinguished from the constrained optimization problems introduced above, in that it aims to identify all the feasible designs instead of the single best feasible one.

Define

• [math]\displaystyle{ k }[/math]: total number of designs;
• [math]\displaystyle{ m }[/math]: total number of performance measure constraints;
• [math]\displaystyle{ c_j }[/math]: control requirement of the [math]\displaystyle{ j }[/math]th constraint for all the designs, [math]\displaystyle{ j=1,2,...,m }[/math];
• [math]\displaystyle{ S_A }[/math]: set of feasible designs;
• [math]\displaystyle{ S_B }[/math]: set of infeasible designs;
• [math]\displaystyle{ \mu_{i,j} }[/math]: mean of simulation samples of the [math]\displaystyle{ j }[/math]th constraint measure and design [math]\displaystyle{ i }[/math];
• [math]\displaystyle{ \sigma_{i,j}^2 }[/math]: variance of simulation samples of the [math]\displaystyle{ j }[/math]th constraint measure and design [math]\displaystyle{ i }[/math];
• [math]\displaystyle{ \alpha_i }[/math]: proportion of the total simulation budget allocated to design [math]\displaystyle{ i }[/math];
• [math]\displaystyle{ \bar{X}_{i,j} }[/math]: sample mean of simulation samples of the [math]\displaystyle{ j }[/math]th constraint measure and design [math]\displaystyle{ i }[/math].

Suppose all the constraints are provided in form of [math]\displaystyle{ \mu_{i,j}\leq c_j }[/math], [math]\displaystyle{ i=1,2,...,k, j=1,2,...,m }[/math]. The probability of correctly selecting all the feasible designs is

[math]\displaystyle{ \begin{align} \mathrm{PCS}=\mathbb{P}\left(\bigcap_{i\in S_A}\Big(\bigcap_{j=1}^m (\bar{X}_{i,j}\leq c_j)\Big) \cap \bigcap_{i\in S_B}\Big(\bigcup_{j=1}^m (\bar{X}_{i,j}\gt c_j)\Big)\right), \end{align} }[/math]

and the budget allocation problem for feasibility determination is given by Gao and Chen (2017)

[math]\displaystyle{ \begin{align} \max_{\alpha_1,\alpha_2,\ldots,\alpha_k} &\mathrm{ PCS} \\ \text{subject to } &\sum_{i=1}^k \alpha_i =1,\\ &\alpha_i\geq 0, i=1,2,...,k. \end{align} }[/math]

Let [math]\displaystyle{ I_{i,j}(x)=\frac{(x-\mu_{i,j})^2}{2\sigma_{i,j}^2} }[/math] and [math]\displaystyle{ j_i\in\mathrm{argmin}_{j\in\{1,...,m\}}I_{i,j}(c_j) }[/math]. The asymptotic optimal budget allocation rule is

[math]\displaystyle{ \begin{align} \frac{\alpha_i}{\alpha_{i'}}=\frac{I_{i',j_{i'}}(c_{j_{i'}})}{I_{i,j_i}(c_{j_i})}, i,i'\in\{1,2,...,k\}. \end{align} }[/math]

Intuitively speaking, the above allocation rule says that (1) for a feasible design, the dominant constraint is the most difficult one to be correctly detected among all the constraints; and (2) for an infeasible design, the dominant constraint is the easiest one to be correctly detected among all constraints.

OCBA with expected opportunity cost

The original OCBA maximizes the probability of correct selection (PCS) of the best design. In practice, another important measure is the expected opportunity cost (EOC), which quantifies how far away the mean of the selected design is from that of the real best. This measure is important because optimizing EOC not only maximizes the chance of selecting the best design but also ensures that the mean of the selected design is not too far from that of the best design, if it fails to find the best one. Compared to PCS, EOC penalizes a particularly bad choice more than a slightly incorrect selection, and is thus preferred by risk-neutral practitioners and decision makers.

Specifically, the expected opportunity cost is

[math]\displaystyle{ \begin{align} EOC=\mathbb{E}_{\mathcal{T}}[\mu_{\mathcal{T}}-\mu_t]=\sum_{i=1,i\neq t}^k \delta_{i,t}\mathbb{P}(\mathcal{T}=i), \end{align} }[/math]

where,

• [math]\displaystyle{ k }[/math] is the total number of designs;
• [math]\displaystyle{ t }[/math] is the real best design;
• [math]\displaystyle{ \mathcal{T} }[/math] is the random variable whose realization is the observed best design;
• [math]\displaystyle{ \mu_i }[/math] is the mean of the simulation samples of design [math]\displaystyle{ i }[/math], [math]\displaystyle{ i=1,2,...,k }[/math];
• [math]\displaystyle{ \delta_{i,j}=\mu_i-\mu_j }[/math].

The budget allocation problem with the EOC objective measure is given by Gao et al. (2017)

[math]\displaystyle{ \begin{align} \min_{\alpha_1,\alpha_2,\ldots,\alpha_k} &\mathrm{ EOC} \\ \text{subject to } &\sum_{i=1}^k \alpha_i =1,\\ &\alpha_i\geq 0, i=1,2,...,k, \end{align} }[/math]

where [math]\displaystyle{ \alpha_i }[/math] is the proportion of the total simulation budget allocated to design [math]\displaystyle{ i }[/math]. If we assume [math]\displaystyle{ \alpha_t \gg \alpha_i }[/math] for all [math]\displaystyle{ i \neq t }[/math], the asymptotic optimal budget allocation rule for this problem is

[math]\displaystyle{ \begin{align} & \frac{\alpha_t^2}{\sigma_t^2}=\sum_{i=1,i \neq t}^k \frac{\alpha_i^2}{\sigma_i^2},\\ & \frac{\alpha_i}{\alpha_j}=\frac{\sigma_i^2/\delta_{i,t}^2}{\sigma_j^2/\delta_{j,t}^2}, i\neq j\neq t, \end{align} }[/math]

where [math]\displaystyle{ \sigma_i^2 }[/math] is the variance of the simulation samples of design [math]\displaystyle{ i }[/math]. This allocation rule is the same as the asymptotic optimal solution of problem (1). That is, asymptotically speaking, maximizing PCS and minimizing EOC are the same thing.

OCBA with input uncertainty

An implicit assumption for the aforementioned OCBA methods is that the true input distributions and their parameters are known, while in practice, they are typically unknown and have to be estimated from limited historical data. This may lead to uncertainty in the estimated input distributions and their parameters, which might (severely) affect the quality of the selection. Assuming that the uncertainty set contains a finite number of scenarios for the underlying input distributions and parameters, Gao et al. (2017) introduces a new OCBA approach by maximizing the probability of correctly selecting the best design under a fixed simulation budget, where the performance of a design is measured by its worst-case performance among all the possible scenarios in the uncertainty set.

Web-based demonstration of OCBA

The following link provides an OCBA demonstration using a simple example. In the demo, OCBA performs and allocates computing budget differently as compared with traditional equal allocation approach.

External links

• Optimal Computing Budget Allocation (OCBA) for Simulation-based Decision Making Under Uncertainty (Simulation Optimization)